La Transformada de Laplace

     La capacidad de obtener aproxiamciones lineales de sistemas físicos permite al analista considerar el uso de la transformación de Laplace. El método de la transformada de Laplace sustituye por ecuaciones algebraicas de resolución relativamente fácil las ecuaciones diferenciales, mas difíciles. La solución para la respuesta temporal se obtiene mediante las siguientes operaciones:

1.- Obtener las ecuaciones diferenciales.
2.- Obtener la transformación de Laplace de las ecuaciones diferenciales
3.- Reslover la transformada algebraica resultante para la variable de interés.

     La transformada de Laplace existe para ecuaciones diferenciales lineales para las que la transformación integral converge. Por lo tanto, a fin de que sea transformable, es suficiente que:

     Para algún número real positivo σ1. Si ka magnitud de f(t) es |f(t)| < Meαt para todo t positivo, la integral convergerá para σ1 < α. Por lo tanto, la región de convergencia viene dada por ∞ > σ1 > α  y σ1 se conoce como abscisa de convergencia absoluta. Las señales que son físicamente realizables siempre tienen una transformada de Laplace. La transformación de Laplace para una función del tiempo, f(t), es:

     La transformada inversa de Laplace se escribe como:

     Las integrales de transformación se han usado para deducir tablas de Laplace que se suelen emplear para la gran mayoría de los problemas. En la tabla siguiente (fuente wikipedia) se dan algunos pares importantes de transformadas de Laplace.
     Alternativamente, la variable s de Laplace se puede considerar como el operador diferencial, de modo que:
                 
         Entonces se tiene también el operador integral: 

ID Función Dominio en el tiempo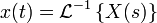
x(t) = \mathcal{L}^{-1} \left\{ X(s) \right\}		 Dominio en la frecuencia
X(s) = \mathcal{L}\left\{ x(t) \right\}		 Región de la convergencia
para sistemas causales
1 retaso ideal \delta(t-\tau) \ e^{-\tau s} \
1a impulso unitario \delta(t) \ 1 \ \mathrm{todo} \ s \,
2 enésima potencia retrasada y con
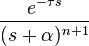desplazamiento en la frecuencia		 \frac{(t-\tau)^n}{n!} e^{-\alpha (t-\tau)} \cdot u(t-\tau) \frac{e^{-\tau s}}{(s+\alpha)^{n+1}} s > - \alpha \,
2a n-ésima potencia 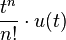{ t^n \over n! } \cdot u(t) { 1 \over s^{n+1} } s > 0 \,
2a.1 q-ésima potencia { t^q \over \Gamma(q+1) } \cdot u(t) { 1 \over s^{q+1} } s > 0 \,
2a.2 escalón unitario u(t) \ { 1 \over s } s > 0 \,
2b escalón unitario con retraso u(t-\tau) \ { e^{-\tau s} \over s } s > 0 \,
2c Rampa t \cdot u(t)\ \frac{1}{s^2} s > 0 \,
2d potencia n-ésima con cambio de frecuencia 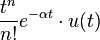\frac{t^{n}}{n!}e^{-\alpha t} \cdot u(t) \frac{1}{(s+\alpha)^{n+1}} s > - \alpha \,
2d.1 amortiguación exponencial e^{-\alpha t} \cdot u(t) \ { 1 \over s+\alpha } s > - \alpha \
3 convergencia exponencial ( 1-e^{-\alpha t}) \cdot u(t) \ \frac{\alpha}{s(s+\alpha)} s > 0\
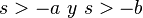3b exponencial doble \frac{1}{b-a}\left(e^{-at}-e^{-bt}\right) \frac{1}{(s+a)(s+b)} s > -a \ y \ s > -b\
4 seno \sin(\omega t) \cdot u(t) \ { \omega \over s^2 + \omega^2 } s > 0 \
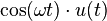5 coseno \cos(\omega t) \cdot u(t) \ { s \over s^2 + \omega^2 } s > 0 \
5b Seno con fase \sin(\omega t+\varphi)\cdot u(t) \frac{ s \sin(\varphi) + \omega\cos\varphi}{s^2+\omega^2} s > 0 \
6 seno hiperbólico 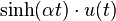\sinh(\alpha t) \cdot u(t) \ { \alpha \over s^2 - \alpha^2 } s > | \alpha | \
7 coseno hiperbólico 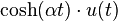\cosh(\alpha t) \cdot u(t) \ { s \over s^2 - \alpha^2 } s > | \alpha | \
8 onda senoidal con
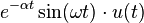amortiguamiento exponencial		 e^{-\alpha t} \sin(\omega t) \cdot u(t) \ { \omega \over (s+\alpha )^2 + \omega^2 } s > -\alpha \
9 onda cosenoidal con
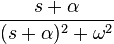amortiguamiento exponencial		 e^{-\alpha t} \cos(\omega t) \cdot u(t) \ { s+\alpha \over (s+\alpha )^2 + \omega^2 } s > -\alpha \
10 raíz n-ésima \sqrt[n]{t} \cdot u(t) s^{-(n+1)/n} \cdot \Gamma\left(1+\frac{1}{t}\right) s > 0 \,
11 logaritmo natural \ln \left ( { t \over t_0 } \right ) \cdot u(t) - { t_0 \over s} \ [ \ \ln(t_0 s)+\gamma \ ] s > 0 \,
12 Función de Bessel
de primer tipo,
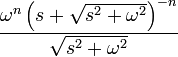de orden n		 J_n( \omega t) \cdot u(t) \frac{ \omega^n \left(s+\sqrt{s^2+ \omega^2}\right)^{-n}}{\sqrt{s^2 + \omega^2}} s > 0 \,
(n > -1) \,
13 Función de Bessel modificada
de primer tipo,
de orden n		 I_n(\omega t) \cdot u(t) \frac{ \omega^n \left(s+\sqrt{s^2-\omega^2}\right)^{-n}}{\sqrt{s^2-\omega^2}} s > | \omega | \,
14 Función de Bessel
de segundo tipo,
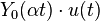de orden 0		 Y_0(\alpha t) \cdot u(t)

15 Función de Bessel modificada
de segundo tipo,
de orden 0		 K_0(\alpha t) \cdot u(t)

16 Función de error \mathrm{erf}(t) \cdot u(t) {e^{s^2/4} \operatorname{erfc} \left(s/2\right) \over s} s > 0 \,

     La transformada inversa de Laplace generalmente se obtiene usando ek desarrollo de fracciones simples de Heaviside. Este método es particularmente útil para el análisis y diseño de sistemas, ya que se puede observar de forma clara el efecto de cada raíz característica o valor propio.

     Estimados visitantes, con el objeto de ilustrar la utilidad de la transformación de Laplace y los pasos necesitados en el análisis de sistemas, consideren el sistema resorte amortiguador descrito en Ecuaciones diferenciales de sistemas


     Se desea obtener la respuesta, y, como una función del tiempo. La transformada de Laplace de la ecuación es:



Cuando



se tiene



Resolviendo para Y(s), se obtiene:



     El polinomio q(s) del denominador, cuando se iguala a cero, se denomina ecuación característica, ya que las raíces de esta ecuación determinan el carácter de la respuesta temporal. Las Raíces de esta escuación también se denominan polos del sistema. Las raíces del polinomio p(s) del numerador se conocen como los ceros del sistema. Los polos y ceros son frecuencias críticas . En los polos, la función Y(s) se hace infinita, mientras que en los cerosla función se hace cero. Los puntos en el plano s de frecuencia compleja de los polos y ceros muestran graficamente el carácter de la respuesta transitoria natural del sistema.

     Par un caso específico, considere el sistema cuando k/M = 2  y  b/M = 3.
     Entonces la ecuación queda:



 En la figura se muestran los polos y ceros de Y(s) en el plano s.

 

     Transformando la ecuación mediante un desarrollo de fracciones simples, se obtiene:



     Donde k1 y k2 son los coeficientes del desarrollo. Los coeficientes, ki, se conocen como residuos y se calculan multiplicando por el factor del denominador de la ecuación que corresponde a ki, y haciendo s igual a la raíz.
Calculando ki cuando y0 = 1, se tiene:

          

Y k2 = -1. Alternativamente, los residuos de Y(s) en los polos respectivos pueden calcularse gráficamente en la representación del plano s, ya que la ecuación anterior puede escribirse como:



     En la figura se muestra la representación gráfica de esta última ecuación:


     El método gráfico para clacular los residuos es particularmente valioso cuando el orden de la ecuación característica es alto y algunos polos son pares conjugados complejos.

     La transformada inversa de Laplace de la ecuación;



       es entonces:

     

      Ahora solo basta usar la tabla, y se obtiene:

     

     Finalmente, suele ser determinar el estado estacionario o valor final  de la respuesta de y(t). Por ejemplo, si se desea calcular la posición en el estado de reposo o estado estacionario del sistema resorte-masa-amortiguador. El teorema del valor final expresa que:


     Donde se permite un solo polo de Y(s) en el origen, pero se excluyen los polos en el eje imaginario en la mitad derecha del plano, y los polos repetidos en el origen. Por lo tanto, para el caso específico resorte-masa-amortiguador, se encuentra que:


     Por consiguiente, la posición final para la masa es la posición de equilibrio normal  y = 0.
     Par ilustrar claramente los puntos principales del método de la transformada de Laplace, se reconsidera el sistema resorte-masa-amortiguador para el caso subamortiguado.
La ecuación para Y(s) puede escribirse como:

 

     Donde ξ es la razón de amortiguamiento adimensional y wn es la frecuencia natural del sistema.  
     Las raíces de la ecuación característica son:
 
      Donde en este caso:
 
     Cuando ξ > 1, las raíces son reales
     Cuando ξ < 1, las raíces son complejas conjugadas

     Cuando ξ = 1, las raíces son repetidas y reales y la condición se llama amortiguamiento crítico
 
  Cuando ξ < 1, la respuesta es subamoriguada y:


     
     En la figura se muestra la gráfica en el plano s de los polos y ceros de Y(s) donde θ = cos-1 ξ. 

Gráfica en el plano s de los polos y ceros de Y(s)

     Cuando ξ varía con wn constante, las raíces complejas conjugadas siguen un lugar geométrico circular, como se muestra en la figura.
     La respuesta transitoria se hace más oscilatoria a medida que las raíces tienden al eje imaginario cuando ξ tiende a cero.

Lugar de las raíces cuando ξvaria con wn constante
     La transformada inversa de Laplace puede calcularse usando el cálculo gráfico del residuo.
     El desarrollo de la ecuación:
    
     en fracciones simples es:
      
     Cuando s2 es el conjugado de s1, el residuo de k2 es el complemento conjugado de k1, por lo cual se obtiene:
 
       Donde el asterisco indica la relación conjugada. El residuo k1 se calcula a partir de la siguiente figura:

  

     La relación directa y clara entre la localización en el plano s de los polos y la forma de la respuesta transitoria se interpreta fácilmente a partir de las gráficas de los polos y ceros en el plano s. Además, la magnitud de la respuesta de cada raíz, representada por el residuo, se visualiza claramente examinando los residuos gráficos en el plano s.
      La transformación de Laplace y el método del plano s son técnicas muy útiles para el análisis y diseño de sistemas cuando se coloca el énfasis en el comportamiento transitorio y en estado estacionario.
     De hecho, como el estudio de los sistemas de control está relacionado principalmente con el comportamiento transitorio y estado estacionario de sistemas dinámicos, tenemos motivos muy válidos para apreciar el valor de las técnicas de la transformada de Laplace.



Gentileza:
El conocimiento es libre. Somos Anónimos. Somos Legión. No perdonamos. No olvidamos. ¡Esperadnos!



No hay comentarios:

Publicar un comentario

Suscribirse a: Entradas (Atom)